|
The emphasis on changes as the carriers of value does not mean that the value of a particular change is independent of the initial position. Value functions are likely to become more linear with increases in assets. A change from $100 to $200 is likely to have a much higher value than a change from $1100 to $1200. The value function is then concave above the reference point (v"(x) < 0 for x > 0), and convex below it (v"(x) > 0 for x < 0). Meaning, it is concave for gains and convex for losses.
Most people dislike symmetric gambles of the sort (50,0.5; -50,0.5). In fact, if x > y 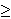 0, then (y,0.5; -y,0.5) is preferred to (x,0.5; -x,0.5). 0, then (y,0.5; -y,0.5) is preferred to (x,0.5; -x,0.5).
This means that v(y) + v(-y) > v(x) + v(-x). Setting y = 0 gives us v(x) < -v(-x), and letting y approach x gives us v'(x) < v'(-x), as long as v is differentiable. So the value function for losses is steeper than that for gains.
|
|
The weighting function π, which relates decision weights to stated probabilities, is an increasing function of p, with π(0) = 0 and π(1) = 1. However, people tend to overweight very small probabilities, like 0.001, so that π(p) > p for very small p.
|