Mini-Ultimatum Game Experiment

Two different approaches can be used in experiments with the Mini-Ultimatum Game.  A simple experiment involving only the Mini-Ultimatum Game (which is Treatment 4 below) will reveal deviations from the economic man model that are consistent with fear and negative reciprocity.  A more complicated experiment involving the Mini-Ultimatum Game and two dictator control games (Treatments 5 and 6 below) discriminates between fear and altruism and between negative reciprocity and inequality aversion. 

Treatments

Treatment 4. Mini-Ultimatum Game

The two players’ payoffs are given by (f, s), where the left number f is the first mover’s payoff and the right number s is the second mover’s payoff. The first mover can choose between Take and Share.  If the first mover chooses Take then the second mover can choose between Tolerate, with payoffs (16, 4), and Punish, with payoffs (0, 0).  If the first mover chooses Share then the second mover can choose between Accept, with payoffs (10, 10), and Reject, with payoffs (0, 0). (In the game tree below and in the game tree in the EFG software for this game, the first mover’s payoff f is the top number and the second mover’s payoff s is the bottom number.)

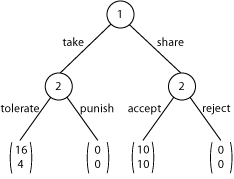
Here is a configuration file for an experiment with this Mini-Ultimatum Game.

 

The more elaborate design that discriminates between fear and altruism and between negative reciprocity and altruism can be implemented with an experiment that includes Treatment 4 (above) and Treatments 5 and 6 (described below).  Here is a configuration file for Treatments 4, 5, and 6.

 

 

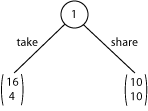
Treatment 5. First Mover Dictator Control for the Mini-Ultimatum Game

The two players’ payoffs are given by (d, n), where the left number d is the dictator’s (“first mover’s”) payoff and the right number n is the non-mover’s payoff.  The dictator can choose between “Take,” with payoffs (16, 4), and “Share,” with payoffs (10, 10).  (In the game tree below and in the game tree in the EFG software for this game, the dictator’s payoff d  is the top number and the non-mover’s payoff n is the bottom number.)

 

Treatment 6.  Second Mover Dictator Control for the Mini-Ultimatum Game

The two players’ payoffs are given by (n, d), where the left number n is the non-mover’s payoff and the right number d is the dictator’s (“second mover’s”) payoff.  The dictator can choose between “Tolerate,” with payoffs (16, 4), and “Punish,” with payoffs (0, 0).  (In the game tree below and in the game tree in the EFG software for this game, the non-mover’s payoff n is the topnumber and the dictator’s payoff d is the bottom number.)

  

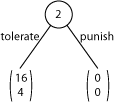
Discussion

• First movers in the Mini-Ultimatum game will split into somewhat unequal size groups of those who choose Take and those who choose Share.

• Between 75% and 90% of the dictators in the first mover dictator control for the Mini-Ultimatum game will choose “Take.”

• Between 5% and 20% of the dictators in the second mover dictator control for the Mini-Ultimatum game will choose “Punish.”

Treatment 4 data

• The homo economicus model predicts: (a) all first movers will choose Take because they only care about their own material payoffs (hence prefer 16 to 10 and 10 to 0) and know second movers have the same type of preferences; and (b) all second movers will choose Tolerate because they only care about their own payoffs (hence prefer 4 to 0).

• Straightforward display of the data reveals actual play of the game by the participants.

Treatment 4 and 5 data

• A natural interpretation of the choice made by a first mover who chooses Share is that the first mover is exhibiting a taste for fairness. But how do we know that the first mover does not actually prefer (16, 4) to (10, 10)? Instead of revealing a taste for fairness by choosing Share, the first mover may be revealing fear that the second mover may punish choice of Take by choosing the outcome (0, 0). Together, Treatments 4 and 5 permit us to address this question. If someone chooses Share in Treatment 4 (the Mini-Ultimatum game) and Take in Treatment 5 (the dictator game) then we can conclude that in Treatment 4 he/she exhibited fear (that the second mover would exhibit negative reciprocity by choosing (0, 0)). If, instead, the first mover chooses Share in both treatments then we can conclude that he/she has altruistic preferences (or, a taste for fairness).

• Straightforward display of the data for both treatments shows how many participants are known to have exhibited fear and how many are know to have exhibited altruism.

Treatment 4 and 6 data

• A natural interpretation of the choice made by a second mover who chooses Punish in the Mini-Ultimatum game is that the second mover is exhibiting negative reciprocity. But how do we know that the second mover prefers (16, 4) to (0, 0)? If the second mover has inequality-averse preferences such that (0, 0) is preferred to (16, 4) then the choice of Punish in the Mini-Ultimatum game does not reveal negative reciprocity. Together, Treatments 4 and 6 permit us to address this question. If second mover chooses Punish in Treatment 4 (the Mini-Ultimatum game) and “Tolerate” in Treatment 6 (the dictator game) then we can conclude that in Treatment 4 he/she exhibited negative reciprocity (he/she chose the outcome that would be dispreferred in the absence of a social norm for negative reciprocity). In contrast, if a second mover chooses Punish in both treatments then he/she is revealing inequality-averse preferences.

• Straightforward display of the data for both treatments shows how many participants are known to have exhibited negative reciprocity.

 

 

 

 

Treatment 4. Mini-Ultimatum Game