http://www.econport.org
   A Digital Library for Microeconomics Education

Copyright © 2006 Experimental Economics Center, Georgia State University. All rights reserved.
 

Most Common Mistakes in Solving Game Theory Problems

This short material illustrates a few typical mistakes that are made in solving Game Theory problems. It is based on examples of simple problems and wrong answers to them. The following material is courtesy Andrzej Skrzypacz Assistant Professor of Economics, Stanford Graduate School of Business .

Mistake 1: Confusing Equilibrium and Equilibrium Outcome.

Question: In the following game identify all pure strategy Nash Equilibria:

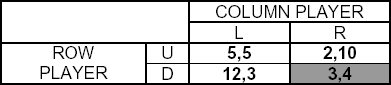
wrong answers:

  1. The NE is (3,4)
  2. The NE is the lower right cell.
  3. The NE is in the shaded cell.
Correct Answer:

  1. The NE is {D,R}.
Especially the first wrong answer is common: (3,4) is the equilibrium outcome not the equilibrium.

Mistake 2: Confusing Equilibrium Strategies And Actions Played Along The Equilibrium Path.

QUESTION: In the following game using backwards induction find all pure strategy Nash equilibria:

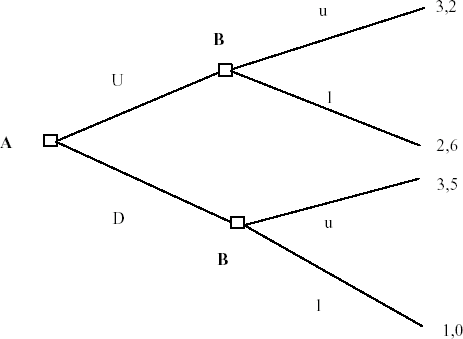
wrong answers:

  1. The NE is that player A will play D and player B will play u.

  2. The NE is (3,5).
Correct Answer:

The NE is: {A plays D; if A plays U - B plays l, if A plays D - B plays u}

The first wrong answer describes only what will happen, not the strategies that players have. To describe an equilibrium you have to describe actions players will take in every decision node, regardless if that node will be reached in equilibrium or not.

The second wrong answer is another example of the first common mistake discussed above.

To write the whole equilibrium can be troublesome if the tree is more complicated. A good way to make it easier is to order the decision nodes. For example in the game:

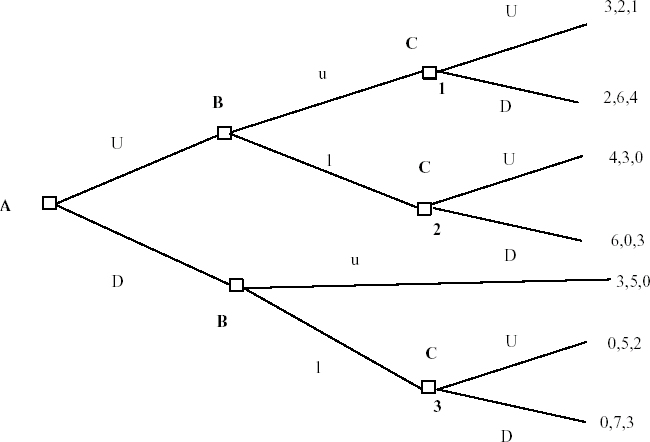
Using backwards induction we can find the NE to be: {A plays U; B plays u in the top decision mode and l in the bottom one; C plays D in the first decision node, D in the second one and D in the third one}.

Mistake 3: Incorrect Reasoning Why Something Is Not A N.E.

Question: In the following game explain why {U,L} is not a Nash Equilibrium.

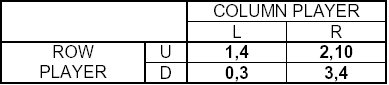
Wrong answers:

  1. {U,L} is not a NE because {D,R} is a NE
  2. {U,L} is not a NE because both players could deviate to {D,R} (which is a NE) and have higher payoffs.
  3. {U,L} is not a NE because the row player could deviate to D knowing that then the column player would choose R instead of L making player 1 better off.


Correct Answer: {U,L} is not a NE because given the Row player plays U, strategy L is not Column player's best response: he would benefit by choosing R instead of L.
This is a very important example as (unlike the mistakes above) it is caused by a mistake in reasoning not by confusion of terms.
The first answer is incorrect because there can be more than one NE in the game.
The second and third answers are incorrect because to verify if some strategy profile is an equilibrium we are supposed to look if any player has a profitable deviation acting on his own i.e. keeping the strategies of all other players fixed.

Mistake 4: Incorrect Usage Of Symmetry Arguement.

Question: Consider a Cournot duopoly game in which there are two firms producing a homogenous good and competing in quantities. The market demand is P=a-bQ, where Q is the sum of outputs: Q=q1 + q2. Both firms have marginal cost equal to c and there are no fixed costs. Find the quantities the firms will choose in a symmetric NE.

Wrong answer: Firm 1 is maximizing its profits: ð1=(P-c)q1.
As the equilibrium is symmetric both firms will produce q1=q2=Q/2.
So the firm solves the following problem: MAX (a-c-bQ)Q/2
This leads to the FOC:
(a-c)/2 - Q=0
So the equilibrium Q=(a-c)/2 so every firm produces (a-c)/4 in the equilibrium.

Correct Answer:
Firm 1 is maximizing profits:
(P-c)q1=(a-c-b(q1+q2))q1.
The F.O.C. of profit maximization is: a-c-bq2-2bq1=0
A similar condition holds for firm 2. To solve this system of equations for the equilibrium quantities we use the symmetry of the equilibrium, which implies that q1*=q2,*. Hence the condition can be rewritten as:
a-c-bq1*-2bq1*=0
Solving yields q1*=(a-c)/(3b).
So the equilibrium outputs are q1*=q2*= (a-c)/(3b).

The mistake in the incorrect answer is that it assumes that firm 1 when making its decision thinks that firm 2 will produce exactly the same output as firm 1 does, regardless of the strategy of firm 1. When firm 1 solves for its best response, it takes the strategy of the other firm as given, so assuming that firm 2 will react by matching the output is incorrect.
A mechanical rule of thumb to remember is to use any symmetry assumptions after Deriving The F.O.C.and never before.

Mistake 5: Incorrect Solution Of The Stackelberg Model

Question:Consider a Stackelberg-leader duopoly model. There are two firms producing homogenous goods and competing in quantities. Firm 1 moves first and firm 2 decides its quantity after observing firm one's decision. The market demand is P=a-bQ, where Q is the sum of outputs: Q=q1 + q2. Both firms have marginal cost equal to c and there are no fixed costs. What output will firm 1 chose? Why?

Wrong answer:

Firm 1 moves first so can disregard firm 2. This implies that firm 1 will act as a monopolist and will produce to maximize:
(a-bq1-c)q1.
The F.O.C. of the profit-maximizing problem is:
a-2bq1-c=0
So the optimal q1*=(a-c)/2b.

Correct Answer:
Firm 1 will take into consideration the fact that firm 2 will react to its choice of output.
Given q1 the best response of firm 2 is to choose q2 to maximize its profits:
(a-bq1-bq2-c)q2.
The F.O.C. of the profit-maximizing problem is:
a-bq1-2bq2-c=0
This implies the best response q2=(a-c-bq1)/2b.
As we said above, firm 1 will take it into consideration and hence its profit-maximizing problem is:
MAX q1 (a-bq1-(a-c-bq1)/2 - c)q1
This can be simplified to:
MAX q1 [(a-bq1-c)/2]q1
The F.O.C. of this problem is:
(a-c)/2 - bq1 = 0
so the optimal q1*=(a-c)/2b

Remember: the whole idea behind the Stackelberg model is that the leader firm foresees the reaction of the follower.

Mistake 6: Forgetting That All Relevant Information Is Already Included In The Payoffs.

Question: In the following game describe the best response of the ROW player to the COLUMN player strategy R:

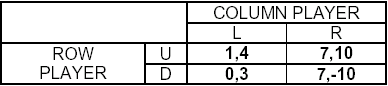
Wrong answer:
Given COLUMN player chooses R the best response of the ROW player is to play D. This strategy provides him the same profits as strategy U but gives lower payoff to his competitor.

Correct Answer:
The best response to strategy R is both U and D. The ROW Player is indifferent between these two strategies so they are BOTH best responses.

If the row values imposing cost on the column player, this value is included in the row player payoff numbers in the payoff table.

Mistake 7: Calling The First Order Condition To Be Best Response Function Or Misspecifying The Best Response Function.

Question: Consider a differentiated product model in which firms compete in quantities and the demand functions are:

P1=a-bq1 - dq2
P2=a-bq2 - dq1.

Find the best response function of firm 1.

Wrong answers:

  1. The profit maximizing problem of firm 1 is:

    MAXq1 [a-bq1 - dq2-c]q1

    The F.O.C. is then: a-c-dq2-2bq1=0.

    This is the best response function.

  2. Manipulating the F.O.C. above we get the best response to be: q2=(a-c-2bq1)/d
Correct Answer:

Using the F.O.C. we get the best response function of firm 1 to be:

q1 = (a-c-dq2)/2b

Notice:

Both the wrong answers can be used to find (correctly) the equilibrium strategies. Nevertheless, Game Theory is a precise science and best response function of firm 1 is supposed to tell us explicitly how the optimal strategy of firm 1 depends on the strategy of firm 2.

Page source: http://www.econport.org/econport/request?page=man_gametheory_mistakes