|
|
|
|
Dictator Controls for Trust Game |
|
The trust game incorporates motives of trust in positive reciprocity and positive reciprocity itself. To test for quantitative effects of these motives one can use a triadic design incorporating dictator controls for trust and for positive reciprocity. |
|
Trust Game Dictator Control 1A (TGDC1A) |
|
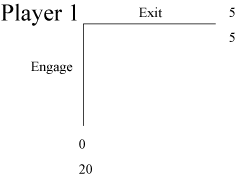
Trust Game Dictator Control 1A is a dictator game in which Player 1 chooses between ($5, $5) and ($0, $20). As noted in Cox and Deck [2002] ?It appears to be a reasonable judgment that any Mover 1 that chooses the monetary payoff pair ($0, $20) instead of ($5, $5) would also choose ($7.50, $12.50) instead of ($5, $5). However, if choices of ($0, $20) were to be observed in Trust Control 1A (here TGDC1A) then it would be necessary to experiment with Trust Control 1B (here TGDC1B) in order do discriminate between first mover motives in the Trust game. The reason is that for a choice of Engage in the Trust game to be interpreted as a trusting action, it must be known that ($5, $5) is preferred to at least one of the payoff pairs that is possible as a result of the player choosing Engage. In the event that all or nearly all subjects in the Trust Control 1A (TGDC1A) choose ($5, $5), the difference between first player decisions in the Trust game and Trust Control 1A (TGDC1A) discriminates between Mover 1?s choices of Engage that are motivated by trust in positive reciprocity and those that are motivated by non-reciprocal other-regarding preferences.? |
|
Overview |
|
|
|
Nash Prediction for Self-Regarding Preferences |
|
An own-payoff maximizing player 1 prefers strategy Exit over Engage since the latter gives him lower payoffs. |
|
Trust Game Dictator Control 1B |
|
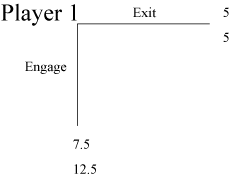
Trust Game Dictator Control 1B corresponds to the following behavior in the Trust game: Player 1 can either Exit or Engage but he knows for sure that if he sends the whole endowment to player 2 it will tripled by the experimenter so after the first stage of the game, player 1 will be left with zero and player 2 with $20. In the second stage player 2 will then decide to share equally the total surplus of $15 created by player 1 and will pass $7.50 back to player 1, which will result in payoffs of ($7.50, $12.50). |
|
Overview |
|
|
|
Nash Prediction for Self-Regarding Preferences |
|
An own-payoff maximizing player 1 strictly prefers strategy Engage over Exit since by choosing it he gets a higher monetary payoff. |
|
Trust Game Dictator Control 2 (TGDC2) |
|
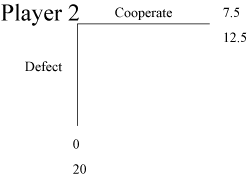
Trust Game Dictator Control 2 is a dictator game in which player 2 chooses between Cooperate, which results in the payoffs ($7.50, $12.50), and Defect, yielding player 2 a $20 payoff and Player 1 a payoff of $0. |
|
Overview |
|
|
|
Nash Prediction for Self-Regarding Preferences |
|
Nash prediction for a player 2 with self-regarding preferences is to Defect since it yields a higher money payoff to oneself than Cooperate. |
|
Common experimental results |
|
Cox and Deck (2002) use a triadic design to discriminate between the motives of trust, positive reciprocity, and other-regarding preferences. In their original Trust Game experiment 13 out of 30 players 1 decided to Exit while 17 others chose to Engage. Out of 17 players 2 who were sent money by paired players 1, 13 Defected and left players 1 with zero and only 4 Cooperated. As Cox and Deck note, these experimental results imply that the trust game is not a very cooperative environment. When comparing the data from the Trust game with the data from Trust Game Dictator Controls (in TGDC1A 28 out of 30 players 1 decided to Exit and only 2 chose Engage; in TGDC2, 20 out of 30 players 2 Defected and 10 decided to Cooperate), they conclude that the choices of players 1 are motivated by trust and that positive reciprocity does not explain behavior of players 2. |
|
Further Readings |
|
|
|
Page source: http://www.econport.org/econport/request?page=man_tfr_experiments_dictgame_trust
|