|
|
|
Ostrom, Gardner, & Walker (1994) conducted a series of experiments designed to test how individual behavior in a common-pool resource framework depends on the institutional setting. Their framework was as follows:
|
|
Within the investment game, individuals are given an endowment of tokens that they can decide to either keep or invest in an investment account. The return on the investment account is determined by the aggregate group investment. For small levels of investment the return exceeds the individual private return. However, if aggregate investment exceeds a given level the return from the investment account becomes less than the individual's private return for not investing. This is achieved using a quadratic return function for the investment account. The functional form is as follows:
|
|
U(i) = w * (e - xi) + [(xi))/(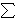 X)]*[ a * ( X)]*[ a * (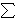 X) - b( X) - b(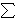 X)^2] X)^2]
|
|
where U(i) is the utility that person i derives within the experiment, w is the private return on an individuals retained endowment, e is the individual endowment, x(i) is person i's investment, (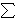 X) is the sum of the groups investment and a and b are coefficients in the quadratic return function. Using this theoretical model and experimental design Ostrom, Gardner, and Walker compared the subject behavior to the symmetric Nash-Equilibrium predictions. Their findings indicate that the individual investment decisions do not follow the symmetric Nash-Equilibrium predictions. X) is the sum of the groups investment and a and b are coefficients in the quadratic return function. Using this theoretical model and experimental design Ostrom, Gardner, and Walker compared the subject behavior to the symmetric Nash-Equilibrium predictions. Their findings indicate that the individual investment decisions do not follow the symmetric Nash-Equilibrium predictions.
|
|
Ebenhöh tested a similar investment game framework. She also introduced a communication treatment, as either a one-shot communication or repeated communication, after the tenth round. A total of 20 to 30 rounds were played. Her setting used the following parameters:
Eight subjects were endowed with 25 tokens. There are two markets; Market 2 is a common resource with a total output of:
Y = 23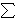 xi -- 0.25( xi -- 0.25(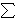 xi)2 xi)2
This total output Y is then divided among the subjects in proportion to the amount of their individual investment, xi, & the rate of return is 1 cent per output token.
All tokens not invested in Market 2 are automatically invested in Market 1, the outside alternative, which has a fixed & constant return of 5 cents per token. Subjects received information about the total investment in the common resource, but not the individual investments of other subjects.
|
|
Theoretical Predictions: The Nash equilibrium strategy is to invest 8 tokens in the common resource, while the group optimum is to invest 4.5 tokens per subject (a total of 36 tokens).
|
|
Total investment tended to follow a pulsing pattern. Investment often started high, yielding negative returns, but then dropped to profitable levels. However, there would soon be overappropriation again, in later rounds, after the return from Market 2 had exceeded the return from Market 1. The variance in yields decreased over time, but there was no stabilization.
Counter to theory which states that communication in these settings is merely "cheap talk", since people cannot be made to keep their word, the one-shot communication treatment did increase the level of co-operation. The net yield was higher, but dropped after a couple of rounds. Repeated communication worked even better, to enable lasting co-operation. However, even in this case, the achieved efficiency was 40% to 80% of the maximum.
The decision heuristics for subjects are fairly complex in this game, given the non-linearity (particularly for a random sample of undergraduates who are not likely to have studied advanced calculus or game theory). The most basic decision rule that subjects used, as they answered in post-experiment questionnaires, was to simply increase the investment when Market 2 yielded a higher return per token than Market 1, & decrease it otherwise. Guessing others' investments led to an opposite, anti-cyclic strategy -- if Market 2 has a higher return per token, assume the others will increase investment, so decrease it yourself. There were others used too, like the mean of previous investments, & other, more sophisticated strategies.
Deadman et al modeled a game similar to the above, using simulations, and found results very similar to those of Ostrom et al.
Catalogued resources for online experiments, including the investment game.
|
- Peter J. Deadman, Edella Schlager and Randy Gimblett (2000). Simulating Common Pool Resource Management Experiments with Adaptive Agents Employing Alternate Communication Routines. Journal of Artificial Societies and Social Simulation, vol. 3, no. 2
- Ebenhöh, Eva. Modeling non-linear common-pool resource
experiments with boundedly rational agents. Institute of Environmental Systems Research, University of Osnabrück, Germany
- Ostrom, E., Gardner R., and J. Walker. (1994), Rules, Games, & Common Pool Resources. The University of Michigan Press.
|
| |