Before we jump into formal discussions of Game Theory, let us take an introductory peek at what Game Theory is all about. The three basic elements of any game are:

• A set of participants, or "players."
• The moves, or "actions," that each player may make.
• The scores, or "payoffs," that each player earns at the end of the game.

Let's consider one of the most talked about games in the Game Theory literature, the prisoner's dilemma. This story can be told a number of ways. It involves two suspected felons, their police interrogators, and their willingness to confess to a crime that it turns out, they did not commit.

Consider two suspects, Mighty Joe and Crazy Crow, who have been brought to the precinct under the suspicion that they were conspirators in the murder of an old lady. Detectives Sherlock Holmes and Hercule Poirot place the two suspects in separate detention rooms and interrogate them one at a time. There is however little evidence which suggests that either was actually involved in the murder, although there is some evidence that they were involved in mugging the victim and stealing her purse.

The two detectives explain to each suspect that they are both looking at jail time for roberry charges, probably for about three years, even if there is no murder confession from either of them. In addition the two smart detectives ell the suspects individually that they "know" what happened and "know" how one has been coerced by the other to participate in the crime. The detectives further hint that jail time for a solitary confessor will be significantly reduced if the whole story is committed to paper. Finally, the prisoners are told that if they both confess, jail terms could be negotiated down but not as much as in the case of one confession and one denial. Both the prisoners then have to decide whether to confess or not confess to the murder.

They both know that no confession leaves them each with a three year jail sentence for robbery. They also know that if one of them confesses, he will get a short sentence for cooperating with the police, while the other will go to jail for 25 years. If both confess, they figure that they can negotiate for jail terms of 10 years each.

What do you think will happen? Do you want to know how a Game Theorist would look at the problem?

The two prisoners are involved in what is known in game theory parlance as a "two person, simultaneous move game" where each has to choose between confessing and not confessing to the crime of murder. The above scenario, with choices and resulting outcomes for the two prisoners can be summarized in a table as below.

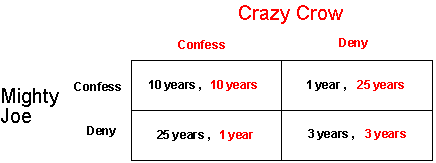
Payoffs to the player choosing the row, Mighty Joe, are listed first in black, and payoffs to the player choosing the column, Crazy Crow, are listed second in red. Payoffs shown are the lengths of the jail sentences associated with each pair of actions from the two prisoners. So in this story, low numbers are better for each player since they indicate fewer years in prison.

Well, how do we know what is best for the two convicts? Let's go ahead and compare the outcomes achieved with each action. For Joe, a confession gets him 10 years in prison if Crow also confesses. Instead, if Joe confesses and Crow does not then Joe only gets a year in prison. An alternative situation for Joe is of not confessing. Well, if Joe does not confess and Crow does, then Joe lands up in jail for 25 years, and if Crow does not confess and Joe does then Joe spends three years behind bars.

Comparing the outcomes we see that confessing is better for Joe if Crow also confesses. Furthermore, confessing is better for Joe if Crow does not confess! So, no matter what Crow does, confessing to the crime is better for Joe. A similar argument holds for Crow. So a solution to this game is that both Joe and Crow decide to confess simultaneously and end up with ten years each in prison. For your information a formal term for a solution like this is "dominant strategy Nash equilibrium."

Continue