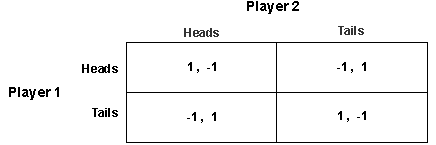
In many games players choose unique actions from the set of available actions. These are called pure strategies .In some situations though a player may want to randomise over several actions. If a player is choosing which action to play randomly, we say that the player is using a "mixed strategy" as opposed to a pure strategy. In a pure strategy a player chooses an action for sure, whereas in a mixed strategy, he chooses a probability distribution over the set of actions available to him. Consider the following game of matching pennies.

Note that this game does not have a pure strategy nash equilibrium: for any pair of pure strategies that the two players choose, one player will receive a negative payoff and hence want to change her strategy choice. So game theorists allow players to have mixed strategies. In particular, let each player play H and T with one-half probability each. We claim then that this choice of strategies constitute an equilibrium, in the sense that if each player predicts that the other player will play in this manner, then he has no reason not to play in the specified manner. Since player 2 plays H with probability ½, the expected payoff of player 1 if he plays H is (1/2)(1) + (1/2) (-1)=0. Similarly the expected payoff to action T is 0. Therefore player 1 has no reason to deviate from playing H and T with probability ½ each. Similarly, if player 2 predicts that player 1 will play H and T with one-half probability each, he has no reason to deviate from doing the same. We say that Player 1 and Player 2 each playing H and T with probabilities ½ and ½ constitutes a mixed strategy equilibrium of the game.

If we assume that players repeatedly play this game and forecast each other?s action on the basis of past play, then each player actually has an incentive to adopt a mixed strategy with these probabilities. If, for example player 1 plays H constantly rather than the above mixed strategy, then it is reasonable that player 2 will come to expect him to play H again and play his best response, which is T. This will result in player 1 getting ?1 as long as he continues playing H. Therefore he should try to be unpredictale, for as soon as his opponent is able to predict his actions he will be able to take advantage of the situation. Similarly player 2 must be unpredictable in order to avoid losing while playing this game.

A mixed strategy for player i is a probability distribution over his set of available actions. In other words, if player i has m actions available, a mixed strategy is an m dimensional vector (α1_i , α2_i ,? αm_i ) such that αk_i >= 0 for all k=1,2,?m, and SUM αk_i =1