|
|
|
Nash equilibrium is one of the central solution concepts for games.
The basic idea of a Nash equilibrium is that if each player chooses
their part of the Nash equilbrium strategy, then no other player
has a reason to deviate to another strategy. A simple example is a
coordination game, such as the one in the figure below.
|
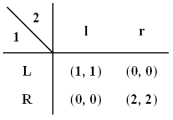
|
|
Figure 1: Coordination game payoffs
|
|
In this game, both (L, l) and (R, r) are Nash equilibria. If Player 1
chooses L then Player 2 gets 1 by playing l and 0 by playing r; if
Player 1 chooses R then Player 2 gets 2 by playing r and 0 by playing
l. The two stratgies L and R for Player 1 and the two strategies l and
r for Player 2 are called "pure strategies" and the strategy pairs
(L, l) and (R, r) are called "pure strategy equilibria."
|
|
Some games, such as Rock-Paper-Scissors, don't have a pure strategy
equilibrium. In this game, if Player 1 chooses R, Player 2 should
choose p, but if Player 2 chooses p, Player 1 should choose S. This
continues with Player 2 choosing r in response to the choice S by
Player 1, and so forth.
|
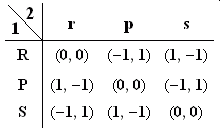
|
|
Figure 1: Rock-Paper-Scissors game payoffs
|
|
In games like Rock-Paper-Scissors, a player will want to randomize over
several actions. If a player randomly chooses a pure strategy, we say
that the player is using a "mixed strategy." In a pure strategy a
player chooses an action for sure, whereas in a mixed strategy, he
chooses a probability distribution over the set of actions available
to him.
|
| |