|
|
|
In this section you will find several public goods exercises and an illustration how to solve them. The following two examples come from the class notes of Professor Mark Walker from the University of Arizona.
|
|
We begin with a simple example of a pure public good. Let's suppose
there are only two people who live on the shore of Lake Magnavista. Amy
likes
to water ski and Bev likes to sunbathe. Both activities are seriously
affected by the level of the water in the lake. When there is a lot of water
in the lake it's good for water skiing, but the water line is so high that
there is no beach for sunbathing. When there is much less water, the
sunbathing is good but the lake is too shallow for water skiing. Thus, Amy
prefers that the lake have lots of water, and Bev prefers that it have much
less water. Fortunately, it is possible to raise or lower the water level
costlessly, by opening a dam at one end of the lake or at the other end.
Unfortunately, it's not clear at what level the water ought to be set.
|
|
In order to have a measure of the amount of water in the lake, let's use
the water's depth at a specified location on the lake: let x denote the
water's depth (in feet) at that location. Amy's and Bev's preferences are
described by the following utility functions:
|
|
uA(x, yA) = yA - (15 - x)2 and uB(x, yB) = yB - 1/2 (6 - x)2,
|
|
where x denotes the water level and yA and yB are Amy's and Bev's daily
consumption of other goods, measured in dollars. Therefore their marginal
rates of substitution are:
|
|
MRSA = 30 - 2x and MRSB = 6 - x.
|
|
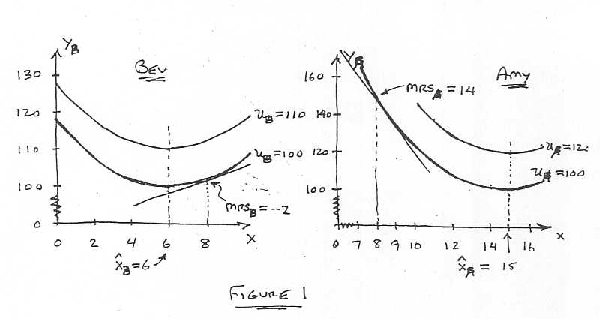
Amy's most-preferred water level is x'A = 15 and Bev's is x'B = 6. Figure 1
depicts their indifference maps. Notice that if the water level is above x'A,
Amy would be willing to pay (i.e., to give up some of the y-good) to have x
reduced, and that Bev would similarly be willing to pay to reduce x if it
were
above her ideal level, x'B. Suppose Amy and Bev each have incomes of $100 per
day.
|
|
|
What makes this situation different than everything we've seen before is
that the x-variable can't be at different levels for different people. It's
not like tacos or beer, where Amy can have one quantity and Bev another. In
this case, the water level can be varied, but it will be the same for both
of
them. That's why we haven't put A and B subscripts on the x-variable; it's
just one variable, not two. The water level in this example is a public
good.
|
|
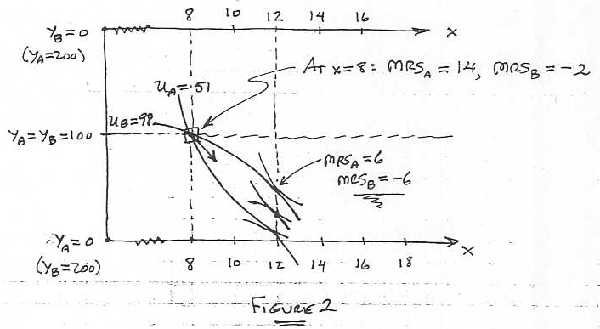
Let's try to determine which outcomes will be Pareto efficient. Figure 2
shows a diagram similar to the Edgeworth Box. The difference is that here in
this diagram the "corners" or "origins" for both individuals are placed on
the
left edge of the diagram, so that when x increases (as we move toward the
right), both individuals' consumption of the x-good is increasing. (This is
in contrast to the Edgeworth Box, in which, as we move toward the right,
Person A's consumption is increasing and B's is decreasing, because with
"private goods" like tacos, the more one person gets, the less remains for
the
other person.)
|
|
|
Let's ask whether a water level of x = 8 feet is efficient. Amy's and
Bev's MRS's will be MRSA = 14 and MRSB = -2. Amy would pay $14 to increase
the water level one foot and Bev would pay $2 to decrease it by one foot
-- or
Bev would accept $2 as compensation for increasing the water level by one
foot. Consequently, if we were to increase the water level by a foot, and if
Amy were to compensate Bev by paying her, say, $6, then both would be better
off. In fact, you can calculate that Amy's utility will increase from 51 to
58 and that Bev's will increase from 98 to 101 1/2.
|
|
So what about the new water level of x = 9 feet? Is it efficient? We
have MRSA = 12 and MRSB = -3, so we could increase the water level by
another
foot, with Amy paying another $6 to compensate Bev. The $6 payment is less
than the $12 Amy would have been willing to pay, and more than the $3 Bev
would have been willing to accept as compensation, so they're again both
better off by the one-foot increase with $6 compensation. You can calculate
that their utilities will have increased again, to uA = 63 and uB = 104.
|
|
Now it is becoming clear that as long as Amy would be willing to pay more
for an increase than Bev would be willing to accept as compensation, then
such
an increase, with compensation paid, will make them both better off. In
other
words, the water level is not efficient so long as MRSA > -MRSB --i.e., so
long as MRSA + MRSB > O. When MRSA + MRSB > 0 the marginal social value of
an
increase in x is positive, so x should be increased. Similarly, we could
show
that if MRSA + MRSB < 0 then x should be decreased (because the marginal
social value of an increase is negative).
|
|
Thus, the Pareto efficient outcomes are the ones that satisfy the Test
Condition MRSA + MRSB = O. In our example, it's easy to solve for the
efficient water level in the lake:
MRSA + MRSB = (30 - 2x) + (6 - x) = 36 - 3x;
therefore the Test Condition yields
36 - 3x = 0 ; i.e., x = 12.
The efficient water level is 12 feet, where MRSA = 6 and MRSB = -6.
|
|
What if there were more than just two people who use the lake? Each
would have some preference involving trade-offs between the desired water
level and consumption of other goods, and therefore an indifference map and
an
MRS schedule, or functon. The Test Condition for Pareto efficiency is the
same as with two people: the sum of all the MRS's (i.e., the marginal social
value of increasing x) must be zero. If the sum were instead positive or
negative, then the water level should be increased or decreased.
|
|
Now we know which water level is Pareto efficient. But what level will
actually be chosen? That depends on the institutional arrangements by which
the water level is chosen. For example, the affected parties might vote on
the level they want. The outcome of that institution can be analyzed using
game theoretic methods, which we won't do here. Let's suppose instead that
Bevowns the lake, or at least that she has the right to choose the water
level. What will the water level be? It seems that Bev will choose the level
that she likes best, namely x = 6 feet.
|
|
But in fact we would expect Bev to bargain or negotiate with Amy to
increase the water level (for a price, to be paid by Amy to Bev). Indeed,
we would expect them to arrive at a mutually agreeable
bargain in which there are no more gains to be had from further trade or
bargaining -- i.e., at a Pareto efficient outcome. In our example this means
that the water level will be 12 feet, with Amy paying Bev some compensation
for the increase from 5 to 12 feet. They will end up at an allocation
somewhere in the football-shaped region formed by their initial indifference
curves.
|
|
What if instead Amy has the right to choose the water level? At first it
seems as if she would choose the level she likes best, x = 15 feet. But the
same argument as above tells us that again they will negotiate to set the
water level at x = 12 feet, but this time with Bev paying Amy some
compensation for setting the level below what she would like the most.
|
|
It was the economist Ronald Coase who pointed out that the assignment of
legal rights will affect only who pays compensation, and how much, but will
not affect the level of the externality-producing activity -- in this case,
the level of the public good, which is the water level.
He was awarded the Nobel Prize for this idea, which has had a profound effect
on law and, to a somewhat lesser extent, on legislation.
|
|
What if the public good is not costless, as in the water level example?
Then the Efficiency Test Condition is that the marginal social value of a
one-unit increase in the amount of the public good must be equal to the marginal
cost of producing that additional unit -- i.e., that the sum of all the MRS's
must be equal to MC:
|
|
MRS1 +MRS2 + ... + MRSn = MC
|
|
Notice that in our lake example the MC of changing the water level was zero,
so this Test Condition is actually the same as the one we used in the
example.
|
|
Example: Suppose Amy and Bev are plagued by mosquitoes, but it is possible
to
control the mosquitoes by spraying regularly. The mosquito spray cannot be
confined to the property of just one of the women: any spray that is used
affects the entire lake shore equally. Suppose Amy's and Bev's preferences
are described by the same utility functions as in our water-level example,
where x now denotes the number of gallons that are sprayed each week, and yA
and yB are Amy's and Bev's weekly incomes. If each gallon of spray were
free,
our problem would be exactly the same as before, because MC = 0. Suppose
instead that the spray costs $24 per gallon. Then our Test Condition yields
the following:
|
|
MRSA + MRSB = MC : (30 - 2x) + (6 - x) = 24 i.e., 36 - 3x = 24.
|
|
Therefore the Pareto efficient amount of spray is 4 gallons per week, which
equates the marginal social value to the marginal social cost. How much will
be sprayed if Amy and Bev each choose on the basis of just their own
personal benefits from the spray? Bev will not choose to spray at all, because even
when x = 0 her MRS is much less than the price of the spray. Amy will choose
x = 3 gallons of spray, which equates her own MRS to the price of the spray.
Thus, too little spray is chosen. Both women would be better off if an
additional gallon were sprayed and, say, Amy paid $22 of the cost and
Bev paid
the remaining $2.
|
|
A More Striking Example: Suppose there are 100 homeowners living on the lake
shore, and that each has MRS = 6 -x, where x is the number of tankfuls that
are sprayed. Suppose that the cost of the mosquito spray is $100 for every
tankful. Then the Pareto efficient amount of spray is x = 5 tankfuls:
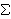 MRSi = MC : 100(6 - x) = 100 i.e., 600 - 100x = 100. MRSi = MC : 100(6 - x) = 100 i.e., 600 - 100x = 100.
|
|
How much will actually be sprayed if each homeowner chooses on the basis of
just his own benefit from the spray? At x = 0 each homeowner has MRS = 6 --
i.e., each would be willing to pay $6 to increase x to one tankful. But the
cost of such an increase -- $100 -- far exceeds each person's MRS. Therefore
no one will choose to spray, and even though the marginal social benefit is
$600 and the marginal social cost only $100, no spray is forthcoming.
|
| |