James Andreoni in "Why Free Ride? Strategies and Learning in Public Goods Experiments," Journal of Public Economics 37, 1988, pp. 291-304, article investigates why free riding is seldom observed in single-shot games but is often approximated in finitely repeated games. He designs a VCM experiment to examine two explanations of such behavior: strategies and learning.

The experimental literature on free riding reports three consistently replicated observations:

1. No significant evidence on free riding in single-shot games.
2. In repeated games, decay of provision of the public good toward free riding level with each repetition.
3. Often approximation of free riding after subjects play several trials, although exact free riding is seldom realized.

Free Riding Hypothesis
Participants, under the assumption of full rationality, should contribute zero towards the public good in both the single-shot and finitely repeated game.

Learning Hypothesis
A single-shot game is not sufficient to allow subjects to learn the free riding incentives. With enough repetition, subjects begin understanding the incentives in the game and choose the individually optimal Nash investment. Thus, repeated play allows for learning what in turn could explain the decay in contributions.

Strategies Hypothesis
In a repeated game setting the subjects might rationally develop multiperiod startegies that allow for some cooperative behavior, even after they learn about the incentives to free ride. It might be an incomplete Nash equilibrium strategy to cooperate early in the game and free ride later in the game. This could be an alternative explanation for the decay in contributions.

Strategic Behavior Example:
If a subject Y believes that her partners might behave irrationally, i.e. invest a positive amount into the public goods because they have not learned the incentives yet, then if she free rides she will educate her partners. As a result, the initial cooperation will shortly change to free riding which gives lower payoffs to the participants. Moreover, if Y believes that her partners think she does not understand free riding, then by contributing zero she would send a signal about her rationality. As a result, any cooperation would unravel to free riding again. Therefore, even if all participants understand free riding, they may choose a strategy of investing in the public good for several periods at the beginning of the game. However, it is always optimal to free ride in the known end-period. The anticipation of the end-period, by using the backward induction argument, causes that the contributions of participants slowly start to decrease.

Andreoni designed this VCM experiment to separate the learning from strategic play. His design is subtractive: "...subjects participate in a repeated-play environment, but are denied the opportunity to play startegically. Without strategic play, we can isolate the learning hypothesis. Furthermore, by comparing this group to one that can play strategically, we can attribute the difference, if any, to strategic play." (Andreoni [1987], pp. 294)

Strangers
In order to be able to subtract the strategies, the subjects were put into one of the two conditions. In the first condition, 20 subjects were randomly assigned to one of 4 groups, each consisting of 5 subjects. Subjects were told they would play 10 rounds and that after each repetition the composition of their group would change in an unpredictable way - the computer would randomly reassign the subjects into the 4 groups. Thus, subjects knew they would be reassigned, but were never told which 4 of the remaining 19 subjects were in their group at any time. This condition ensures that subjects could not gain by playing strategically. Andreoni calls this treatment a "repeated single-shot game" and since the subjects meet randomly, they are called "Strangers."

Partners
At the same time 15 different subjects were placed in an adjacent room. In groups of 5 they played a standard finitely repeated game, playing with the same subjects in every round. They knew the composition of their group was fixed, but they did not know which 4 of the remaining 14 subjects belonged to their group. Since they played with the same subjects all the time, they were called "Partners" and constituted a control group to Strangers, because they could play startegically. Except for the only difference in group composition, both Partners and Strangers faced exactly the same game.

Payoffs
Each subject was given an endowment of 50 tokens. Each token invested in the public good earned 0.5 cent for each subject in the group, regardless of who invested it. Each token kept privately by an individual earned 1 cent but only for this particular person. Earnings in each round were set aside and could not be used in later rounds.

Suppose a subject is initially contributing a positive amount towards the public good, but in some period t she learns that free riding is a single-shot [LINK dominant strategy]. If she is a Partner and plays strategically, she might have an incentive to continue contributing. However, if she is a Stranger, there is no reason for her to invest in the public good since every game is the end-game for her. Therefore, under the strategic hypothesis, it is expected that Partners will be contributing more than Strangers, especially early in the game before the Partners start to decrease their contributions because of the game-end effect. In the last round, both groups are predicted to free ride.

To isolate the learning effect, the experimental design included a restart followed by three rounds of play. Partners were told they would stay in the same group, while Strangers would continue to be randomly reassigned as before. Under the learning hypothesis, both Partners and Strangers should not be affected by the restart. If behavior of either group would change, it would imply that learning itself is not primarely responsible for decay.

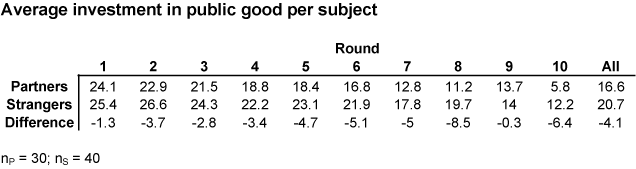
Observation 1. Contributions by Partners are significantly smaller than contributions by Strangers in all 10 rounds and the difference grows as the last round approaches. This is exactly the opposite to the strategies hypothesis indicating that giving by Partners should be greater in all rounds with the difference getting smaller towards the end of the game.

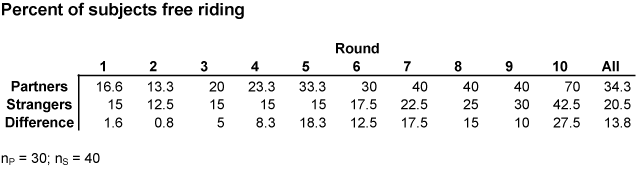
Observation 2. In all 10 rounds the percent of free riding Partners is greater than the percent of free riding Strangers. The difference is greatest in the last round and is statistically significant. This opposes the strategies hypothesis.

Observation 3. The contributions by Partners are smaller in round 10, but are still above the free riding level, again contradicting the strategies hypothesis.

Observation 4. The contributions by Strangers are greater that contributions by Partners in the last round. In round 10 the incentives are the same for both groups, and, moreover, they have had the same opportunity for learning. Nevertheless, Strangers invest significantly more, and free ride significantly less. This result does not support the learningn hypothesis.

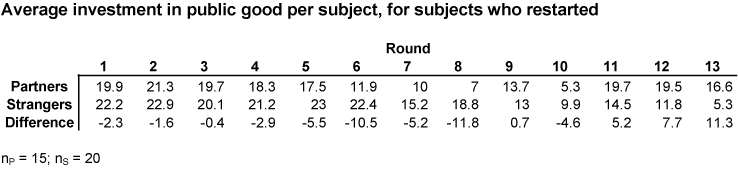
Observation 5. Strangers appear to be only temporarily affected by the restart.

Observation 6. Partners return to high contributions after the restart. The restart also seems to have a lasting effect on this group. On the other hand, the Strangers were not affected as strongly and treated the restart as a continuation of the repeated single-shot game. Since the learning hypothesis predicts that both Partners and Strangers should be uneffected by the restart, it suggests that there might actually be little learning about free riding, and that subjects mostly understand the incentives from the start. As Andreoni notes, subjects given the opportunity to repeat their choices, they by and large do so. Hence, learning is also unlikely to provide an explanation of decrease in contributions towards the end of the game.

Based on observations 1-6, both rational strategic play and learning hypotheses are contradicted in this study. Andreoni suggests that perhaps the hypotheses do not focus on the right kind of learning. It is possible that subjects have learned the single-shot dominant strategy, but have not learned the backward induction necessary to understand the equilibrium. Also an understanding of the single-shot equilibria does not necessarily reveal an understanding of the repeated-game structure. The results also suggest that one might want to consider an alternative to monetary payoff maximizing model, for example subjects getting non-monetary pleasure from cooperative outcomes or investing being consistent with social norms about participation in social dilemmas. Decay in this case might represent the groups' struggles to establish a norm. For further discussion on alternatives to monetary payoff maximizing model, see the section on Trust, Fairness, and Reciprocity.