|
In their 1992 paper, Kahneman and Tversky developed an updated form of prospect theory, which they termed Cumulative Prospect Theory. The theory incorporates rank-dependent functionals which transform cumulative, rather than individual probabilities, in response to a growing literature, and satisfies stochastic dominance, which the original form of prospect theory does not. It retains the most crucial features, though, viz.:
- Gains and losses, i.e. income is the carriers of value, not final assets or wealth.
- The value of each outcome is multiplied by a decision weight, not an additive probability.
|
|
A risky prospect f is a function that maps states of the world s 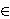 S into consequences x S into consequences x 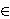 X. Outcomes of prospects are arranged in increasing order, so that a prospect f is represented by a sequence of pairs (xi, Ai), and yields xi if Ai occurs, where Ai is a partition of S. X. Outcomes of prospects are arranged in increasing order, so that a prospect f is represented by a sequence of pairs (xi, Ai), and yields xi if Ai occurs, where Ai is a partition of S.
A prospect is called strictly positive or strictly negative if all its outcomes are positive or negative respectively. It is labeled positive or negative if all its outcomes are non-negative or non-positive, respectively. All other prospects are called mixed. We have the positive part of f, f+(s) = f(s) if f(s) > 0, and f+(s) = 0 if f(s) 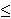 0. The negative part of f, f-(s) = f(s) if f(s) < 0, and f-(s) = 0 if f(s) 0. The negative part of f, f-(s) = f(s) if f(s) < 0, and f-(s) = 0 if f(s) 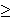 0. 0.
A number V is assigned to each prospect, so that f 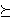 g if & only if V(f) g if & only if V(f) 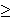 V(g). V(g).
A capacity W is a function that assigns to each A 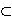 S a number W(A) satisfying W( S a number W(A) satisfying W(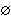 ) = 0, W(S) = 1, & W(A) ) = 0, W(S) = 1, & W(A) 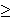 A(B) when ever A A(B) when ever A 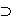 B. B.
There exists a strictly increasing value function v:X 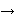 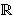 , satisfying v(x0) = v(0) = 0, and capacities W+ & W-, such that for f = (xi, Ai), -m , satisfying v(x0) = v(0) = 0, and capacities W+ & W-, such that for f = (xi, Ai), -m 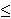 i i 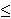 n: n:
V(f) = V(f+) + V(f-)
V(f+) = 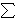 nv=0 nv=0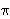 +i +i
V(f-) = 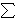 nv=-m nv=-m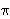 -i -i
If the prospect f is defined by a probability distribution p(Ai) = pi, then the decision weights 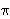 +(f+) = ( +(f+) = (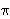 +0... +0...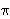 +n) and +n) and 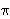 -(f-) = ( -(f-) = (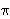 --m... --m...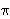 -0) are defined by: -0) are defined by:
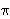 +n = w+(pn) +n = w+(pn)
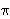 --m = w-(p-m) --m = w-(p-m)
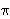 +i = w+(pi + ... + pn) - w+(pi+1 + ... + pn), 0 +i = w+(pi + ... + pn) - w+(pi+1 + ... + pn), 0 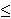 i i 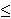 1; 1;
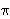 -i = w-(p-m + ... + pi) - w-(p-m + ... + pi-1), 1-m -i = w-(p-m + ... + pi) - w-(p-m + ... + pi-1), 1-m 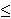 i i 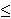 0. 0.
where w+ & w- are strictly increasing functions from the unit interval into itself, & they satisfy w+(0) = w-(0) = 0, & w+(1) = w-(1) = 1.
|
|
The decision weight 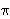 +i is the difference between the capacities of the events "the outcome is at least as good as xi," and "the outcome is strictly better than xi." +i is the difference between the capacities of the events "the outcome is at least as good as xi," and "the outcome is strictly better than xi."
The decision weight 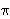 -i is the difference between the capacities of the events "the outcome is at least as bad as xi," and "the outcome is strictly worse than xi." -i is the difference between the capacities of the events "the outcome is at least as bad as xi," and "the outcome is strictly worse than xi."
In this manner, the decision weight associated with each outcome is the marginal contribution of the event defined in terms of the capacities. If each capacity W is additive, it is a probability measure & so 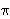 i is simply the probability of Ai. i is simply the probability of Ai.
For both positive and negative prospects, the decision weights add to 1, but the sum can be greater or less than 1 for mixed prospects. This is because the decision weights for gains & losses are defined by different capacities.
|
|
As in the original version of prospect theory, v is assumed concave above the reference point 0 -- the boundary between gains and losses -- and convex below it, so that v"(x) 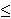 0 for x 0 for x 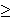 0, and v"(x) 0, and v"(x) 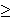 0 for x 0 for x 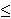 0. 0.
Also, v is steeper for losses than gains, so that v'(x) < v'(-x) for x 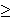 0. This principle is called diminishing sensitivity -- the further the distance from the reference point, the smaller the impact of a change. So the impact of a change in probability diminshes with its distance from the boundary -- a change in probability from 0.9 to 1 has a greater impact than a change from 0.6 to 0.7. The weighting function is therefore concave near 0 and convex near 1. 0. This principle is called diminishing sensitivity -- the further the distance from the reference point, the smaller the impact of a change. So the impact of a change in probability diminshes with its distance from the boundary -- a change in probability from 0.9 to 1 has a greater impact than a change from 0.6 to 0.7. The weighting function is therefore concave near 0 and convex near 1.
|
|
Tversky, Amos & Kahneman, Daniel (1992). "Advances in Prospect Theory: Cumulative Representation of Uncertainty." Journal of Risk & Uncertainty. 5:297-323.
|