|
|
|
In 1944, John Von Neumann and Oskar Morgenstern published their book, Theory of Games and Economic Behavior. In this book, they moved on from Bernoulli's formulation of a utlity function over wealth, and defined an expected utility function over lotteries, or gambles. Theirs is an axiomatic derivation, meaning, a set of assumptions over people's preferences is required before one can construct a utility function.
|
|
von Neumann and Morgenstern weren't exactly referring to Powerball when they spoke of lotteries (although Powerball is one of many kinds of gambles that the theory describes). In their definition, a lottery or gamble is simply a probability distribution over a known, finite set of outcomes. These outcomes could be anything - amounts of money, goods, or even events. In this framework, we know for certain what the probability of the occurrence of each outcome is.
Getting back to our earlier examples, we can frame them as:
- For the Derby betting pool, the set of outcomes A = {Santa's Little Helper wins, Santa's Little Helper doesn't win}
- For the pharmaceutical company, the set of outcomes A = {Earn $500 million from patent, Earn $200 million from patent, Earn $0 from patent}
|
|
Each of these outcomes had a probability attached to it, and so we can define a simple lottery as a set of outcomes, A={a1, a2,...,an} each of which occurs with some known probability pi.
We can then also construct compound lotteries, which are probability distributions over lotteries - i.e., an outcome of a lottery may itself be another lottery. As a concrete example, imagine a Powerball lottery where the prize is yet another lottery ticket. Let G represent the set of all lotteries, or gambles, both simple and compound.
|
|
In order to construct a utility function over lotteries, or gambles, we will make the following assumptions on people's preferences. We denote the binary preference relation "is weakly preferred to" by 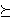 , which includes both "strictly preferred to", and "indifferent to". , which includes both "strictly preferred to", and "indifferent to".
- Completeness: For any 2 gambles g and g' in G, either g
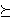 g' or g' g' or g' 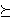 g. In English, this means that people have preferences over all lotteries, and can rank them all. g. In English, this means that people have preferences over all lotteries, and can rank them all.
- Transitivity: For any 3 gambles g, g', and g" in G, if g
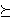 g' and g' g' and g' 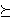 g", then g g", then g 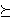 g". In English, if g is preferred (or indifferent) to g', and g' is preferred (or indifferent) to g", then g is preferred (or indifferent) to g". g". In English, if g is preferred (or indifferent) to g', and g' is preferred (or indifferent) to g", then g is preferred (or indifferent) to g".
- Continuity: Mathematically, this assumption states that the upper and lower countour sets of a preference relation over lotteries are closed. Along with the other axioms, continuity is needed to ensure that for any gamble in G, there exists some probability such that the decision-maker is indifferent between the "best" and the "worst" outcome. This may seem irrational if the best outcome were, say, $1,000, and the worst outcome was being run over by a car. However, think of it this way - most rational people might be willing to travel across town to collect a $1,000 prize, and this might involve some probability, however tiny, of being run over by a car.
- Monotonicity: This big ugly word simply means that a gamble which assigns a higher probabilty to a preferred outcome will be preferred to one which assigns a lower probability to a preferred outcome, as long as the other outcomes in the gambles remain unchanged. In this case, we're referring to a strict preference over outcomes, and don't consider the case where the decision-maker is indifferent between possible outcomes.
- Substitution: If a decision-maker is indifferent between two possible outcomes, then they will be indifferent between two lotteries which offer them with equal probabilities, if the lotteries are identical in every other way, i.e., the outcomes can be substituted. So if outcomes x and y are indifferent, then one is indifferent between a lottery giving x with probability p, and z with probability (1-p), and a lottery giving y with probability p, and z with probability (1-p). Similarly, if x is preferred to y, then a lottery giving x with probability p, and z with probability (1-p), is preferred to a lottery giving y with probability p, and z with probability (1-p).
Note: This last axiom is frequently referred to as the Independence axiom, since it refers to the Independence of Irrelevant Alternatives (IIA).
The last axiom allows us to reduce compound lotteries to simple lotteries, since one can also be similarly indifferent between a a simple lottery giving an outcome x with a probability p, and compound lottery where the prize might be yet another lottery ticket, allowing one to participate in a lottery with x as a possible outcome, such that the effective probability of getting x was p.
|
|
A utility function u is said to have the expected utility property if, for a gamble g with outcomes {a1, a2,...,an}, with effective probabilities p1, p2,...,pn respectively, we have:
u(g) = p1u(a1) + p2u(a2) + ... + pnu(an)
where u(ai) is the decision-maker's utility from outcome ai.
An individual who chooses one gamble over another if and only if the expected utility is higher is an expected utility maximizer.
|
|
von Neumann and Morgenstern proved that, as long as all the preference axioms hold, then a utility function exists, and it satisfies the expected utility property. See here for a complete proof of the Expected Utility Theorem.
As it stands, expected utility theory is widely used in theoretical and practical analysis - see the section on Applications of Expected Utility Theory for a detailed discussion. However, it is not without its flaws; in particular, many experiments have shown that people routinely violate the behavioral axioms. These have now become famous paradoxes in themselves - see the experimental discussion of the Allais Paradox and the Ellsberg Paradox.
|
|
By convention, we use the term Bernoulli Utility Function to refer to a decision-maker's utility over wealth - since of course it was Bernoulli who originally proposed the idea that people's internal, subjective value for an amount of money was not necessarily equal to the physical value of that money. The term von Neumann-Morgenstern Utility Function, or Expected Utility Function is used to refer to a decision-maker's utility over lotteries, or gambles.
Continue: Risk Aversion
|
| |
|
|
|