|
|
|
Other-regarding preferences refer to preferences over another individual's material payoffs, in addition to one's own. Such preferences incorporate notions of fair divisions. Below we present three categories of other-regarding preferences and introduce the literature definitions of their particular types.
|
|
Distributive
- Bolton [1991], Bolton and Ockenfels [2000], Fehr and Schmidt [1999]
|
|
Reciprocal
- Fehr, Kirchsteiger, and Riedl [1993], Berg, Dickhaut, and McCabe [1995]
|
|
Both Distributive and Reciprocal
- Bolton and Ockenfels [2000], Charness and Rabin [2002], Cox and Friedman [2002], Dufwenberg and Kirchsteiger [2004], Falk and Fischbacher [1999]
|
|
Formal Example:
Consider the case of two agents and let yj and yk denote the money payoffs of agents j and k. If agent k's preferences can be represented by a utility function, then agent k has other-regarding preferences for the income of agent j if his utility function, uk(yk , yj) is not a constant function of yj. Such preferences can be altruistic or inequality-averse. The preferences are altruistic if the utility function, uk is globally increasing in both arguments [Cox, Sadiraj, Sadiraj, 2001]. The preferences are inequality-averse if uk is increasing in yk, decreasing in max(0, yj - yk), and possibly also decreasing in max(0, yk-yj) [Fehr and Schmidt, 1999].
|
|
Fehr and Schmidt Model of Inequity Aversion [1999]
An individual is inequity averse if she dislikes inequitable outcomes. The fairness judgements are based on a neutral reference point given by social comparison processes. The model assumes that in addition to pure selfish players, there exist players who dislike inequitable outcomes who suffer more from the disadvantageous inequity than from the advantageous one.
Consider a two-player case. The utility function of player i is given by:
Uk(yk, yj) = yk - 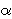 k max {yk - yj, 0} - k max {yk - yj, 0} - 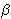 k max {yk - yj, 0}, k k max {yk - yj, 0}, k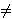 j j
where y denotes the vector of respective monetary payoffs and 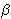 k k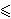 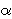 k and 0 k and 0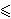 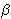 k<1. The second term in k's utility function measures the degree of utility loss from disadvantageous inequality and the third term the utility loss from advantageous inequality. k<1. The second term in k's utility function measures the degree of utility loss from disadvantageous inequality and the third term the utility loss from advantageous inequality. 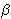 k k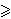 0 rules out the existence of players who like to be better off than others. To interpret the restriction on model parameters that 0 rules out the existence of players who like to be better off than others. To interpret the restriction on model parameters that 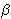 k<1, suppose player k has a higher monetary payoff than player j. If k<1, suppose player k has a higher monetary payoff than player j. If 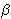 k = 0.5, then player k is just indifferent between keeping $1 for himself and giving this $1 to player j. If k = 0.5, then player k is just indifferent between keeping $1 for himself and giving this $1 to player j. If 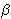 k=1, then player k is willing to destroy this $1 to reduce his higher payoff relative to player j what seems implausible. k=1, then player k is willing to destroy this $1 to reduce his higher payoff relative to player j what seems implausible.
If there are n > 2 players, player k compares herself with all other n-1 players. In such case the second and third terms of k's utility function are normalized by dividing by n-1. This way the relative impact of inequality aversion of player k's total payoff is independent of the number of players. The model also assumes that the disutility from inequality is self-centered, i.e. player k compares herself with each of the other players but does not care about the inequalities between the pairs of her opponents.
|
|
Read about Berg, Dickhaut, and McCabe [1995] study here.
|
|
Fehr, Kirchsteiger, and Riedl [1993]
|
|
Cox and Friedman [2002]
|
|
Dufwenberg and Kirchsteiger [2004]
|
| |