|
|
|
|
|
In this discussion we present a triadic (three-games) experimental design developed by James C. Cox, Klarita Sadiraj, and Vjollca Sadiraj in "Implications of Trust, Fear, and Reciprocity for Modeling Economic Behavior" [2004] to discriminate between actions motivated by unconditional preferences over the distribution of material outcomes and actions motivated by attributions of the intentions of others and beliefs about their behavior.
|
|
The section on Trust, Fairness, Reciprocity, and Other-Regarding Preferences presents many examples of human behavior inconsistent with the self-regarding preferences model's predictions. Such actions can be motivated by conditional preferences (beliefs- and/or intentions-conditional preferences over outcomes) or by beliefs- and/or intentions-unconditional (for example, altruistic or inequality-averse) preferences. Cox, Sadiraj, and Sadiraj [2004] use a triadic design including a moonlighting game and two specially designed dictator games, as control treatments, to separate the actions motivated by unconditional other-regarding preferences from actions dependent on beliefs about others and/or attributions of their intentions.
|
|
The experiment was run with the use of computer software. It included three treatments described below in an across-subject design (different population if subjects participated in each of the three treatments.) Since the sessions were run in CREED laboratory at the University of Amsterdam, all money payoffs as well as feasible choices were quoted in euro. A double-blind social distance protocol that guaranteed the complete social isolation of the subject's decision, that is no one including other subjects, experimenter or any outside observer could possibly learn any individual's behavior in the experiment.
was implemented. The instructions referred to the subjects as being type X or type Y, corresponding to being the first or the second mover. The use of evocative verbs, such as "send", "return", "give", "take", "reward", and "punish" were avoided. The feasible actions were presented to subjects in tables explaining the effects of increasing and decreasing the interdependent account balances of both movers.
|
|
Treatment A
Treatment A is the moonlighting game. The endowment of both movers is 10 euro. The first mover can either give money to the second mover or take money from him/her. Maximum amount that can be passed is the whole endowment of the first player, maximum amount taken, however, is only 5 euro, i.e. one-half of the second mover?s endowment. Money given is increased by a multiplicative factor equal to 3, while any amount taken is not transformed. After the second mover learns about the outcome of stage 1 (i.e. about the tripled amount sent or the amount taken) he/she has an opportunity also to give or take money from the first mover. Each euro given by the second mover to the first mover costs the second mover one euro and each euro taken by the second mover from the first mover costs the second mover 1/3 euro. All choices made by first and second movers are required to be integer amounts.
|
|
|
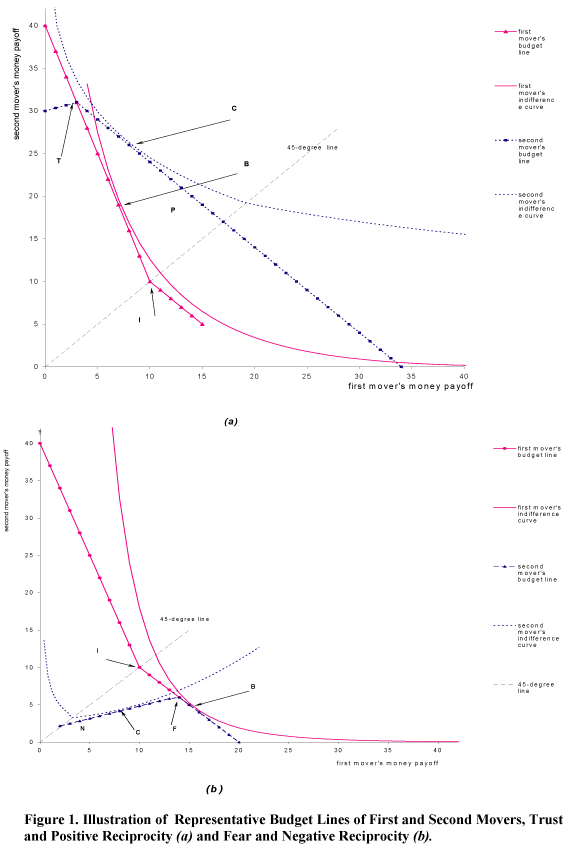
Source: James C. Cox, Klarita Sadiraj, and Vjollca Sadiraj, "Implications of Trust, Fear, and Reciprocity for Modeling Economic Behavior," University of Arizona discussion paper, 2004. [CSS]
|
|
"Figure 1.a shows representative choices open to the subjects in treatment A. The piece-wise-linear solid line passing through points T, B, and I is the first mover's "budget line." The two subjects' endowments are at point I, the intersection of the first mover's "budget line" and the 45-dege line. The slope of the first mover's "budget line" is -3 above the 45-degree line and -1 below the 45-degree line. The first mover's choice of an integer amount to give to or take from the second mover determines the second mover's "budget line." If the first mover were to give 7 euro to the second mover, she would change the two subjects' endowments from (10, 10) to (3, 31), indicated by point T in Figure 1.a. This choice by the first mover would determine the second mover's "budget line" shown by the piece-wise-linear dashed line with a kink at point T in Figure 1.a. The slope of the second mover's "budget line" is + 1/3 below the first mover's budget line and -1 above it. If instead, the first mover were to take 4 euro from the second mover then the second mover's "budget line" would be the piece-wise-linear dashed line with a kink at point F in Figure 1.b.
|
|
In treatment A, the first mover chooses a "budget line" for the second mover by choosing an integer amount to give or take from the second mover. Subsequently, the second mover chooses a point on this "budget line" that determines both first- and second-mover money payoffs. The second mover's choice is an integer amount to give to or take from the first mover." [Cox, Sadiraj, and Sadiraj, 2004, pp. 4]
|
|
Treatment B
Treatment B is the moonlighting game dictator control 1 (MGDC1). It is a variation of the moonlighting game when the second mover has no decision to make, i.e. the first mover becomes a dictator. Thus the first mover can either give money to the second mover or take money from her. The maximum amount that can be given is the whole endowment of the first player; the maximum amount taken, however, is only 5 euro, i.e. half of the second mover?s endowment. Money given is multiplied by 3, while any amount taken is not transformed. The game ends after the first mover made her choice. This choice determines the money payoffs for both subjects.
The moonlighting game dictator control 1 eliminates the possible motives of trust in positive reciprocity and fear of negative reciprocity that might be present in player 1?s behavior when playing the original moonlighting game. Altruism is the only positive motive for the first mover to send a positive amount in this dictator treatment.
|
|
Treatment C
Treatment C is the moonlighting game dictator control 2 (MGDC2). The first mover has no decision to make and the second mover is given an initial endowment (10 euro) plus additional money equal to the amount that she would receive in the moonlighting game, corresponding to one of the "budget lines" determined by a first mover's decision in treatment A. The dictators (second movers) were not told that the additional amount was selected by first movers in the moonlighting game to avoid possible indirect reciprocity effects. They were informed about the relation between the additional amount they receive and the endowment of the randomly and anonymously paired first mover. The second mover's strategy is the same as in the moonlighting game and the only difference is that the observed allocation was not generated by the paired first mover. The second mover then chooses an integer amount on her "budget line" to give or take from the paired first mover.
The moonlighting game dictator control 2 eliminates the possible motives of positive reciprocity and negative reciprocity that might be present in players? behavior in the moonlighting game.
|
|
Trusting Behavior
"A trusting action is an action that generates a profit that can be shared and requires a belief by the first mover that the second mover will not defect and keep to much of the profit." [Cox, Sadiraj, and Sadiraj, 2004, pp. 9] However, if the first mover decides to send a positive amount of money, it does not necessarily mean that she exhibits trusting behavior, unless it is known that she has self-regarding or inequality-averse preferences. Alternative explanation of sending a positive amount to the second mover are altruistic preferences. In such case, the first mover might prefer to give some money regardless of how much, if any, the second mover might return. The examination of choices in treatment A moonlighting game together with the treatment B moonlighting 1 dictator control allows to identify the trusting behavior. Suppose tht the amount sent by the first mover to the second mover in treatment A is positive (sa>0) and greater than the amount sent in treatment B (sa>sb) which does not necessarily have to be positive. Since the only reason for sending a positive amount in treatment B is altruism, one can conclude that the first mover exhibited trust because the amount sent in treatment A is greater than the unconditional preferences could explain.
"Figure 1.a illustrates a trusting action by a first mover with altruistic preferences. An example of an altruistic choice, sb>0 is shown by the tangency of the first mover's indifference curve with his "budget line" at the point B in Figure 1.a. An example of a trusting choice sa(>sb>0) is shown by the point T in Figure 1.a. This choice gives the second mover the piece-wise-linear dashed budget line with a kink at point T. If the second mover chooses any amount to return that would result in some money allocation below the first mover's indifference curve passing through point B, then the first mover is worse off than she would have been if she had, instead, chosen sa=sb (at point B in Figure 1.a) and the second mover had returned, for example, any amount of money from 0 to 2sb" [Cox, Sadiraj, and Sadiraj, 2004, pp. 10]
|
|
Positively-Reciprocal Behavior
There are two possibilities why the second mover may return part of the tripled money to the first mover. One explanation are the preferences over payoff pairs conditional on a social norm for reciprocating the intentionally generous behavior of the first mover. By returning some or all money, the second mover repays a generous action with a generous response. The other explanation for sending back a positive amount to the first mover are unconditional altruistic or inequality-averse other-regarding preferences. The treatment A moonlighting game together with the treatment C moonlighting dictator control 2 allows to separate positively-reciprocal behavior from unconditional preferences.
"Consider a second mover in treatment C who is given an endowment that is larger than the endowment of the paired subject. The endowments of a pair of subjects in treatment C are determined by a (distinct) first mover's decision in treatment A, sa (but the subjects do not know this). In treatment C, a second mover chooses an amount to return, rc from a feasible set of integers on the piece-wise-linear "budget line" determined by a first mover's choice of sa in treatment A. An example of a possible choice, rc is shown by the tangency of the second mover's indifference curve with her "budget line" at point C in Figure 1.a." [Cox, Sadiraj, and Sadiraj, 2004, pp. 11]
Suppose in the moonlighting game the second mover returns a positive amount to the first mover. Such a choice does not necessarily indicate that the second mover is motivated by a positive reciprocity because her action could have been motivated by unconditional altruistic preferences as well. A positive reciprocity is present in the second mover's behavior if one observes that the second mover returned more in treatment A moonlighting game than in treatment C (ra>0 and ra>rc) because the amount returned in the moonlighting game is greater than the unconditional other-regarding preferences could explain.
|
|
Fearful Behavior
A fearful behavior refers in this context to a fear of negatively-reciprocal. It is based on a belief of the first mover that the second mover has either inequality-averse preferences and/or will punish the first mover for taking money. To identify whether the first movers in the moonlighting game who do not trust take less money (if they do so) from the second movers when the second movers have an opportunity to retaliate comparing to a situation when the second movers do not have a choice to make.
Suppose that the first mover takes money from the second mover in the moonlighting game. If the first mover takes more money in tratment B, when she is a dictator and the second mover does not have a chance to punish, than in treatment A (sb< sa=< 0), it follows that the first mover's behavior is motivated by fear. Again, the reason is that the amount taken in treatment A is too small to be explained by unconditional preferences.
"Figure 1.b illustrates behavior of a fearful first mover. In that figure the first mover's choice in treatment B is at the tangency point B whereas point F is the first's mover choice in treatment A. Point F is on a lower unconditional indifference curve for the first mover than is point B. The choice of F in the moonlighting game is evidence that the first mover is afraid to choose his most preferred outcome point B in the moonlighting game." [Cox, Sadiraj, and Sadiraj, 2004, pp. 13]
|
|
Negatively-Reciprocal Behavior
There are two possible explanations why the second mover took money from
the first mover: preferences over payoff pairs conditional on social norm of punishing the intentionally unfriendly behavior of the first mover and/or unconditional inequality-averse preferences. In the first case, by taking some or all money from the first mover, the second mover retaliates to the greedy action. In the second case, the second mover may prefer a costly action to decrease the money payoff of the first mover who has a greater money endowment. The treatment A moonlighting game together with the treatment C moonlighting dictator control 2 allows to separate negatively-reciprocal behavior from unconditional preferences.
"Consider a "second mover" in treatment C who is given an endowment that is smaller than the endowment of the paired subject. Recall that the endowments of a pair of subjects in treatment C are determined by a (distinct) first mover's decision in treatment A, sa (but the subjects do not know this). In treatment C, a "second mover" chooses an amount to return, rc from a feasible set of integers on a piece-wise-linear "budget line" determined by a first mover's choice of sa in treatment A. Suppose that the second mover makes a costly decision ra<0 which reduces the first mover's money payoff in the moonlighting game, treatment A by 3|ra|. This, in itself, does not support the conclusion that the second mover was motivated by negative reciprocity because the assumed choice could have been motivated by unconditional inequality-averse preferences, as shown by the tangency of the upward-sloping part of the indifference curve at point C in Figure 1.b. However, if in addition one observes that rac then he can conclude that the second mover was motivated by negative reciprocity because the hostile action is too costly to be fully accounted for by unconditional (inequality-averse) preferences. In Figure 1.b, any location of ra on the second mover's "budget line" that is downwards and to the left of point C would exhibit negative reciprocity." [Cox, Sadiraj, and Sadiraj, 2004, pp. 14]
|
|
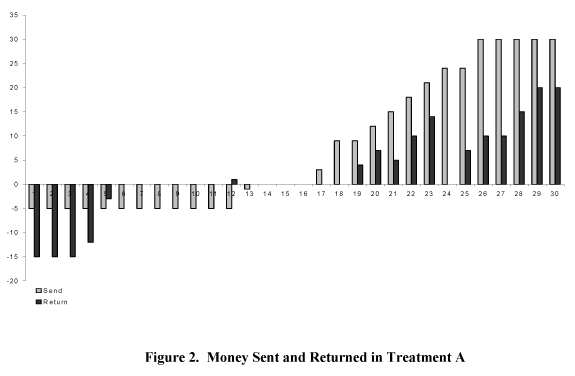
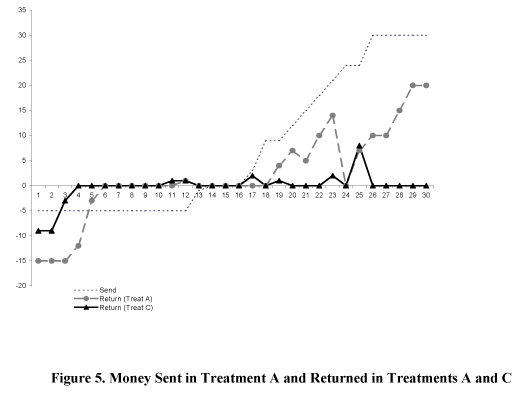
In the moonlighting game experiment Cox, Sadiraj, and Sadiraj [2004] observe that the behavior of the first movers is characterized by trust in positive reciprocity and they also notice that the first movers are not afraid of negative reciprocity: 12 out of 30 players 1 took the maximum possible amount of 5, 1 player took 2, 3 players "sent" zero and 14 players gave positive amounts to the paired player 2.
|
|
|
Source: CSS
|
|
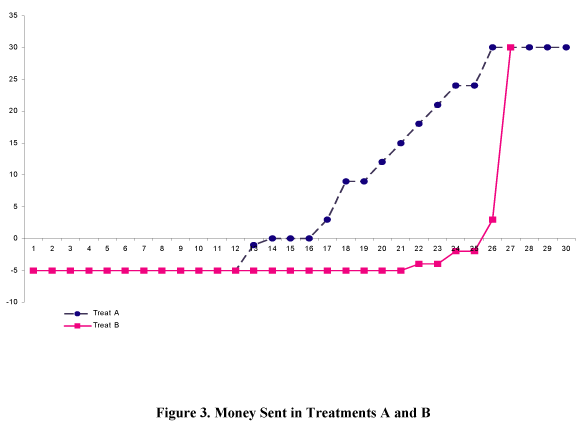
In MGDC1 25 out of 27 players 1 took money and only two players exhibited altruism by sending positive amounts. Thus, the behavior of players 1 is not characterized by significant altruism. Furthermore, it can be concluded from the study that behavior of only 11% of first movers is consistent with fear of negative reciprocity and 47% exhibited trust.
|
|
|
Source: CSS
|
|
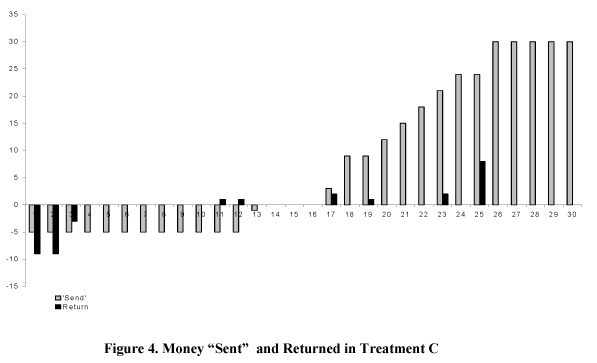
In the same study 14 second movers received positive amounts of money sent by paired players 2 in moonlighting game and were provided these amounts by the experimenters in MGDC2. In the moonlighting game 11 returned positive amounts to players 1 and 3 kept all the money. In MGDC2 11 players 2 kept all the money and only 3 returned some positive amounts. The comparison of the data suggests that the behavior of second movers in the moonlighting game is characterized by significant positive reciprocity.
|
|
|
Source: CSS
|
|
|
Source: CSS
|
| |