|
|
|
The following example describes a pair of choices that are inconsistent with regularity properties P.1 - P.4 for preferences.
Suppose that a person, faced with the same two budget sets that you faced in the choice example,
selects the consuption levels indicated in figure 5 below.
|
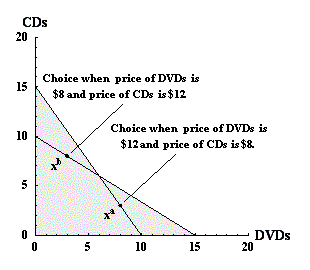
Figure 5: Choices that are inconsistent with regular preferences.
|
|
Intuitively, the problem with this pattern of choices is that, when the price of CDs is low (pCD = 8) and the price of DVDs is high (pDVD = 12), the consumption of DVDs exceeds the consumption of CDs, and when the price of CDs is high, and the price of DVDs is low, the consumption of CDs is high, and the consumption of DVDs is low.
|
|
The inconsistency in the choices xa and xb in figure 5 with the properties of preferences is demonstrated with a simple argument.
- When the prices of CDs and DVDs are pCD = 8 and pDVD = 12 then the consumption choices are shown by point xa. Call the prices for this budget pa. For these prices, xa uses the consumer's entire budget, but xb leaves part of the budget unused, so pa xa > pb xb. Consequently, xa is chosen when xb is available, so xa must be at least as good as xa. Strict monotonicity (property P.4) implies that there is a point x' near xb that is preferred to xb and x' is also affordable when xa is chosen. So xa
 x' (since xa is chosen when x' is available), and x' x' (since xa is chosen when x' is available), and x' 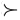 xb. Therefore, xa xb. Therefore, xa
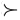 xb. xb.
- When the prices of CDs and DVDs are pCD = 12 and pDVD = 8 then the consumption choices are shown by point xb. Call the prices for this budget pb. In this case, xb uses the consumer's entire budget, but xa leaves part of the budget unused, so pb xb > pa xa. In this case, an argument similar to the one above shows that xb
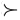 xa. xa.
- Transitivity can be applied to these two observations to demonstrate that these choices are inconsistent. Since xa
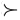 xb, and xb xb, and xb
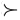 xa, by transitivity (property P.3), xa xa, by transitivity (property P.3), xa
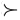 xa. This violates reflexivity (property P.2), so the choices described in the example of figure 5 are inconsistent with properties P.1 through P.4. xa. This violates reflexivity (property P.2), so the choices described in the example of figure 5 are inconsistent with properties P.1 through P.4.
|
|
One of the motivations for the properties of preferences is that, for a consumer whose preferences exhibit the regularity properties P.1 through P.4, and one additional property called continuity, the consumer's preferences can be represented by a utility function, and utility functions are useful because it is possible to evaluate changes in a consumer's choice patterns when the consumer's choice set varies. One important example of a consumer's response to changes in the choice set is a demand function.
In the next section, an argument is developed that shows that if a consumer's preferences satisfy P.1 through P.4 and contnuity, then her preferences can be represented by a demand function u(x) such that u(x) > u(y) if and only if x 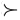 y. y.
|
|
Go to Representation of Preferences by a Utility Function. (A)
Skip to Examples of Consistent Choices. (I)
|
| |