|
For the
choice example with two commodities, when prices change, the choice of a consumer typically changes as well. The example of inconsistent choices demonstrates that not all patterns of choice are consistent with the preference properties P.1 - P.4.
|
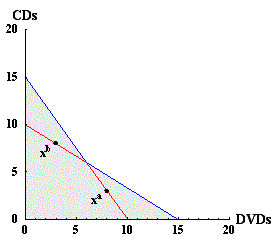
Figure 7: Regions where choices are consistent or inconsistent.
|
|
In the example of inconsistent choices, both choices lie along the portion of the budget that is shown in red in figure 7. In the analysis that demonstrates that the pattern of choices xa and xb is inconsistent with the properties of preferences, the argument depends on the fact that xa is chosen when xb is available, and xb is chosen when xa is available. This can only happen when the choices lie in the red part of the budget lines in figure 7. (Strong monotonicity implies that each choice lies on the budget line rather than in the interior of the budget set, so that if the two choices were on the red portion of the budget set, there would be one on each of the two segments.) If either of the two choices lies on the blue part of the budget lines, then there is a utility function that is consistent with the choices.
There are three different ways that at least one of the choices can be on the blue portion of the budget line. Examples of utility functions that are consistent with choices are shown for each of these three cases in the figures below.
|
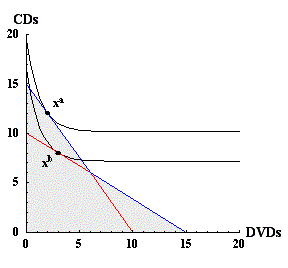
Figure 8: Utility function that rationalizes choices xa and xb.
|
|
Figure 8 shows an example of two consumption choices that are consistent with a utility function. In this example, xa is now on the blue portion of its budget set.
|
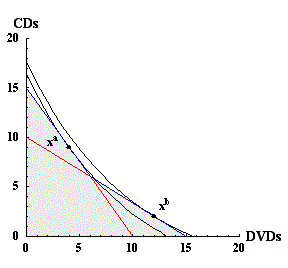
Figure 9: Utility function that rationalizes choices xa and xb.
|
|
Figure 9 shows another example of two consumption choices that are consistent with a utility function. In this example, xa is on the blue portion of its budget set, and xb is also on the blue portion of its budget set.
The last case is similar to the case in figure 8, but and xa is on the red part of its budget set and and xb is on the blue portion of its budget set. This case is really the same as the one in figure 8 though, with the labels and axes for xa and xb interchanged.
|
|
These examples are intended to convey the idea that utility functions can be used to generate many patterns of choices, though not all choices can come from maximization of a utility function. The next section, which describes some of the basic results from "revealed preference" theory, approaches in a more formal way this question of when observations can be rationalized by a utility function.
|
|
Next.
|
| |