|
There are two additional relations, called indifference and strict preference that can be defined in terms of the preference relation  . Both of these relations inherit
the properties of . Both of these relations inherit
the properties of  . In order to prove the existence of a utility function that represents choice, transitivity of the strict preference relation is needed. . In order to prove the existence of a utility function that represents choice, transitivity of the strict preference relation is needed.
|
|
Two consumption levels x and x' are indifferent if x  x' and if x' x' and if x'  x. This is typically written x x. This is typically written x 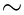 x'. x'.
Indifference is transitive because the relation  that it is derived from is transitive. that it is derived from is transitive.
Proof: If x 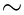 x' and x' x' and x' 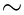 x'', then
from the definition of indifference above, x x'', then
from the definition of indifference above, x  x'
and x' x'
and x'  x'' so that x x'' so that x  x'', and
also x'' x'', and
also x''  x' and x' x' and x'  x so that
x'' x so that
x''  x. Taken together, this shows that if
x x. Taken together, this shows that if
x 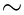 x' and x' x' and x' 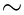 x'' then x x'' then x 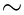 x''. x''.
|
|
Consumption level x is strictly preferred to consumption level x' if x  x' and x' and 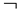 x' x'  x. (The symbol x. (The symbol 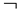 mean "not".) In words, x is at least as good as x', but x' is not at least as good as x. This leaves only the possibility that x is strictly preferred to x', which we write as x mean "not".) In words, x is at least as good as x', but x' is not at least as good as x. This leaves only the possibility that x is strictly preferred to x', which we write as x 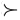 x'. x'.
Strict preference inherits transitivity from  . .
Proof: Let x and x' be such that x 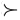 x' and x' x' and x' 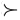 x''. Then the strict preference relation x''. Then the strict preference relation 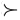 is transitive if this implies that x is transitive if this implies that x 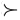 x''. x''.
From the definition of strict preference, x 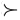 x' if and only if x x' if and only if x  x' and x' and  (x' (x'  x). Similarly, x' x). Similarly, x' 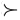 x'' if and only if x' x'' if and only if x'  x'' and x'' and 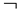 (x'' (x'' 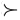 x'). From x x'). From x  x' and x' x' and x'  x'' and transitivity of x'' and transitivity of  we get x we get x  x''. Suppose that x'' x''. Suppose that x''  x. Since x x. Since x  x' this would imply, again by transitivity of x' this would imply, again by transitivity of  , that x'' , that x''  x'. But x' x'. But x' 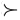 x'' which by definition implies that x'' which by definition implies that 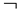 (x'' (x''  x'). This contradicts the assumption that x'' x'). This contradicts the assumption that x''  x, so x x, so x 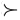 x'' and x'' and 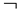 (x'' (x''  x), which is equivalent to x x), which is equivalent to x 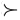 x''. x''.
|